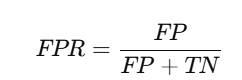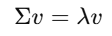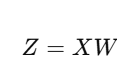क्या आपको पता है कि Machine Learning Engineers इस समय में सबसे ज़्यादा paid tech professionals हैं?
इनकी average salary लगभग £100k है — जो software engineers, AI engineers, और data scientists से भी ज़्यादा है।
लेकिन ध्यान दें दोस्तों, बात सिर्फ़ salary की नहीं है।
एक Machine Learning Engineer के तौर पर आपको मिलती है:
- Fascinating problems को हल करने का मौका
- Cutting-edge tools के साथ प्रयोग करने का अवसर
- दुनिया पर positive impact डालने की satisfaction
तो इस article में, मैं आपको एक clear और simple learning roadmap दूँगा जिससे आप Machine Learning Engineer बन सकते हैं। साथ ही, मैं आपको best resources भी बताऊँगा।
चलिए शुरू करते हैं! 🚀
🧮 Maths और Statistics
मैंने ये बात कई बार कही है — लेकिन अगर आप Machine Learning या पूरे Data Field में करियर बनाना चाहते हैं,
तो Maths और Statistics सबसे ज़्यादा ज़रूरी चीज़ें हैं जो आपको सीखनी चाहिए।
Technologies आती-जाती रहती हैं — जैसे Blockchain या AI,
लेकिन Mathematics सदियों से एक मूल आधार (fundamental staple) बना हुआ है।
अच्छी बात ये है कि आपको Maths Genius होने की ज़रूरत नहीं है।
मैं अपने first-hand experience से कह सकता हूँ कि Machine Learning में काम करने के लिए बस उतनी ही maths चाहिए
जितनी आपको school के आखिरी सालों या undergraduate STEM degree के पहले-दूसरे साल में सिखाई जाती है।
📘 3 Main Areas of Focus
- Linear Algebra (रेखीय बीजगणित) →
इसमें आप matrices, eigenvalues, vectors जैसी चीज़ें सीखते हैं।
ये concepts हर जगह इस्तेमाल होते हैं — जैसे Principal Component Analysis (PCA), TensorFlow,
यहाँ तक कि एक dataframe भी एक तरह की matrix ही होती है। - Calculus (कलन) →
इससे आप differentiation सीखते हैं — यानी कैसे gradient descent और backpropagation algorithms अंदर से काम करते हैं।
ये हर machine learning algorithm के training और learning process में उपयोग होते हैं। - Statistics (सांख्यिकी) →
इसमें आप सीखेंगे: probability, distributions, Bayesian statistics, Central Limit Theorem, और Maximum Likelihood Estimation
इन तीनों में से Statistics सबसे ज़्यादा valuable है। अगर आप शुरुआत कर रहे हैं, तो अपना ज़्यादातर ध्यान Statistics पर ही दें।
🐍 Python
Python को Machine Learning की मुख्य भाषा माना जाता है —
कई beginners और मेरे coaching clients में मैंने देखा कि लोग हमेशा “best Python course” ढूँढते रहते हैं।
मैं दोहराऊँगा – “best” जैसा कुछ नहीं होता।
कोई भी popular Python introduction course चलेगा क्योंकि सब में लगभग वही concepts सिखाए जाते हैं।
🔑 Python Basics
- Native Data Structures →
dict,tuple,list - Loops →
forऔरwhile - Conditional Statements →
if-else - Functions और Classes
- Common Libraries
- Design Patterns
🧠 Python Packages for ML
- NumPy → Arrays के लिए numerical computing
- Pandas → Data manipulation और analysis
- Matplotlib → Data visualization और plotting
- Scikit-learn → Fundamental ML algorithms implement करने के लिए
- SciPy → General scientific computing के लिए
📚 Python Resources
- W3Schools Python Course
- Python for Everybody Specialisation
- Machine Learning with Python and Scikit-Learn
🧩 SQL
एक Machine Learning Engineer के लिए SQL भी बहुत जरूरी है।
खासकर जब आप datasets बनाते हैं या feature engineering करते हैं।
मैं अपने अनुभव से कह सकता हूँ कि मैं लगभग 30–40% समय SQL में बिताता हूँ।
यानी ये बहुत ज़रूरी skill है।
📘 SQL Topics to Learn
SELECT * FROM,ASALTER,INSERT,CREATE,UPDATE,DELETEGROUP BY,ORDER BYWHERE,AND,OR,BETWEEN,IN,HAVINGAVG,COUNT,MIN,MAX,SUMFULL JOIN,LEFT JOIN,RIGHT JOIN,INNER JOIN,UNIONCASE,IFFDATEADD,DATEDIFF,DATEPARTPARTITION BY,QUALIFY,ROW()
📚 SQL Resources
- The Complete SQL Bootcamp: Go from Zero to Hero
- W3Schools SQL Tutorial
- TutorialsPoint SQL Tutorial
Free resources काफी हैं, इसलिए course खरीदने की ज़रूरत नहीं।
और अगर कहीं अटक जाएँ, तो ChatGPT हमेशा मदद कर सकता है। 💡
🤖 Machine Learning
Machine Learning Engineer बनने के लिए ML algorithms सीखना बेहद जरूरी है।
ये roadmap का fun part है और ज्यादातर लोग इसी कारण इस field में आते हैं।
सच कहूँ तो, इन algorithms को सीखना हमेशा fun नहीं होता।
थोड़ा mental effort और समय लगता है, लेकिन धीरे-धीरे सब समझ में आ जाएगा और मेहनत worth it होगी।
🔑 Key Algorithms और Concepts
- Linear, Logistic और Polynomial Regression
- Generalised Linear Models (GLM) और Generalised Additive Models (GAM)
- Decision Trees, Random Forests, Gradient-Boosted Trees
- Support Vector Machines (SVM)
- K-Means और K-Nearest Neighbour Clustering
- Feature Engineering (categorical features)
- Evaluation Metrics
- Regularisation, Bias vs Variance Tradeoff, Cross-Validation
- Gradient Descent और Backpropagation
📚 ML Resources
- Machine Learning Specialisation by Andrew Ng → Best starter course
- The Hundred-Page ML Book → Concise और practical
- Hands-On ML with Scikit-Learn, Keras, and TensorFlow → Entry/mid-level ML engineers के लिए complete guide
🧠 Deep Learning
Fundamental ML algorithms ही career में सबसे ज़्यादा काम आते हैं।
लेकिन Deep Learning important है:
- NLP (Natural Language Processing)
- Computer Vision
Areas to Study
- Neural Networks → ML की foundation
- Convolutional Neural Networks (CNNs) → Image detection
- Recurrent Neural Networks (RNNs) → Time series और NLP
- Transformers → Current state-of-the-art
Resources
- Deep Learning Specialization by Andrew Ng
- Neural Networks: Zero to Hero (YouTube) → Andrej Karpathy
- Deep Learning (Adaptive Computation and ML series) → Yoshua Bengio
🛠 Software Engineering
Machine Learning Engineer बनने के लिए software engineering fundamentals जानना जरूरी है।
Areas
- Data Structures & Algorithms → Arrays, Linked Lists, Queues, Sorting, Binary Search, Trees, Hashing, Graphs
- System Design → Networking, APIs, Caching, Proxies, Storage
- Production Code → Typing, Linting, Testing, DRY, KISS, YAGNI
- APIs → ML models को API endpoints के रूप में serve करना
☁️ MLOps
Jupyter Notebook में model का business value नहीं है।
आपको deploy करना सीखना होगा।
Learn
- Cloud → AWS, GCP, Azure
- Containerisation → Docker, Kubernetes
- Version Control → Git, GitHub
- Shell/Terminal →