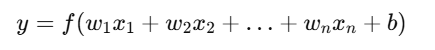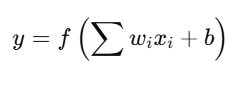Anand Singh

(हानि फलन और अनुकूलन विधियाँ)

---

🔷 1. Loss Function (हानि फलन) क्या है?

Loss function यह मापता है कि आपके मॉडल की prediction असली output से कितनी दूर है।

🔁 Role in Training:

• Prediction → Loss Function → Error → Backpropagation → Weight Update

📌 कार्य:

Step	कार्य
Prediction	Output generate करना
Loss	गलती मापना
Backpropagation	Gradient निकालना
Optimizer	Weights update करना

---

🔹 2. Loss Function के प्रकार

🔸 A. Regression Problems के लिए:

✅ Mean Squared Error (MSE):

• Continuous values के लिए
• Output को penalize करता है अगर prediction और label का अंतर बड़ा हो

✅ Mean Absolute Error (MAE):

• Outliers से कम प्रभावित

---

🔸 B. Classification Problems के लिए:

✅ Binary Cross Entropy:

L=−[ylog⁡(p)+(1−y)log⁡(1−p)]

• Binary classification के लिए
• Sigmoid + BCELoss

✅ Categorical Cross Entropy:

• Multi-class classification
• Softmax + CrossEntropyLoss

---

💻 PyTorch Examples:

import torch
import torch.nn as nn

# MSE Loss
mse_loss = nn.MSELoss()
pred = torch.tensor([2.5])
target = torch.tensor([3.0])
print("MSE:", mse_loss(pred, target).item())

# Binary Cross Entropy
bce_loss = nn.BCELoss()
pred = torch.tensor([0.9])
target = torch.tensor([1.0])
print("BCE:", bce_loss(pred, target).item())

---

🔧 3. Optimization (अनुकूलन)

Optimizer वह algorithm है जो model के weights को loss minimize करने के लिए update करता है।

---

🔸 4. Common Optimization Algorithms

Optimizer	Description
SGD	Simple gradient descent
Momentum	Adds momentum to SGD updates
RMSProp	Adaptive learning rate, good for RNN
Adam	Adaptive + Momentum = Most widely used

---

🔁 Gradient Descent Update Rule:

जहाँ:

• η: Learning rate
• ∂L/∂w: Gradient of loss w.r.t. weights

---

⚠️ Learning Rate की भूमिका:

Learning Rate	परिणाम
बहुत छोटा	Slow training
बहुत बड़ा	Overshooting, unstable
सही	Fast & stable convergence

---

💻 PyTorch में Optimizer:

import torch.optim as optim

model = torch.nn.Linear(1, 1)
optimizer = optim.Adam(model.parameters(), lr=0.01)

# Example training step:
loss = torch.tensor(0.5, requires_grad=True)
loss.backward()
optimizer.step()
optimizer.zero_grad()

---

🎯 Objectives Summary

• Loss function prediction error को मापता है
• Optimizers gradients का उपयोग कर weights को update करते हैं
• PyTorch में loss + optimizer combo सबसे जरूरी सेटअप है

---

📝 अभ्यास प्रश्न (Practice Questions)

1. Loss Function और Optimizer में क्या अंतर है?
2. MSE और MAE में क्या अंतर है?
3. Binary Cross-Entropy का फॉर्मूला लिखिए
4. Adam Optimizer कैसे काम करता है?
5. नीचे दिए गए कोड का output क्या होगा?

loss = torch.tensor(1.0, requires_grad=True) loss.backward() print(loss.grad)

(सक्रियण फलन: Sigmoid, Tanh, ReLU)

---

🔷 1. परिचय (Introduction)

Neural Network में Activation Function यह तय करता है कि कोई neuron “active” होगा या नहीं।
यह non-linearity लाता है, ताकि मॉडल complex patterns को सीख सके।

---

🔹 2. आवश्यकता क्यों? (Why Needed?)

बिना Activation Function के neural network एक simple linear model बन जाएगा।

📌 With Activation Function → Deep, non-linear models
📌 Without Activation → सिर्फ linear transformation

---

🔶 3. मुख्य Activation Functions

---

🔸 A. Sigmoid Function

📌 Output Range: (0, 1)
📌 उपयोग: Binary classification, Logistic regression

✅ लाभ:

• Probability की तरह आउटपुट देता है
• Smooth gradient

❌ कमी:

• Gradient vanishing problem
• Output range छोटा है

📈 ग्राफ: S-shaped (S-curve)

---

🔸 B. Tanh (Hyperbolic Tangent)

📌 Output Range: (-1, 1)
📌 उपयोग: जब input data zero-centered हो

✅ लाभ:

• Stronger gradients than sigmoid
• Centered at 0 → better learning

❌ कमी:

• Still suffers from vanishing gradient (large input पर gradient → 0)

📈 ग्राफ: S-shaped but centered at 0

---

🔸 C. ReLU (Rectified Linear Unit)

📌 Output Range: [0, ∞)
📌 उपयोग: Deep Networks में सबसे आम activation

✅ लाभ:

• Fast computation
• Sparse activation (only positive values pass)
• No vanishing gradient for positive inputs

❌ कमी:

• Dying ReLU Problem: negative input → always zero gradient

📈 ग्राफ: 0 for x < 0, linear for x > 0

---

🔁 तुलना तालिका (Comparison Table)

Feature	Sigmoid	Tanh	ReLU
Output Range	(0, 1)	(-1, 1)	[0, ∞)
Non-linearity	✅	✅	✅
Vanishing Gradient	Yes	Yes	No (partial)
Speed	Slow	Slow	Fast
Usage	Binary outputs	Hidden layers (earlier)	Deep models (most common)

---

💻 PyTorch Code: Activation Functions

import torch
import torch.nn.functional as F

x = torch.tensor([-2.0, 0.0, 2.0])

print("Sigmoid:", torch.sigmoid(x))
print("Tanh:", torch.tanh(x))
print("ReLU:", F.relu(x))

---

🎯 Learning Summary (सारांश)

• Sigmoid और Tanh smooth functions हैं लेकिन saturation (vanishing gradient) से ग्रस्त हो सकते हैं
• ReLU simple, fast, और deep networks में सबसे अधिक उपयोगी है
• Hidden layers में ReLU सबसे लोकप्रिय choice है

---

📝 अभ्यास प्रश्न (Practice Questions)

1. Sigmoid और Tanh में क्या अंतर है?
2. ReLU का गणितीय फॉर्मूला क्या है?
3. Dying ReLU problem क्या है?
4. यदि input -3 हो तो ReLU का output क्या होगा?
5. नीचे दिए गए PyTorch कोड का आउटपुट बताइए:

x = torch.tensor([-1.0, 0.0, 1.0]) print(torch.tanh(x))

(परसेप्ट्रॉन और मल्टी-लेयर परसेप्ट्रॉन)

---

🔷 1. Perceptron: Single-layer Neural Unit

➤ परिभाषा:

Perceptron एक single-layer feedforward neural network है जो binary classification करने में सक्षम होता है।

🧮 गणितीय रूप:

---

📌 विशेषताएँ:

गुण	विवरण
Structure	एक ही layer (input से output)
Use	Linear binary classification
Limitation	Non-linear problems (जैसे XOR) solve नहीं कर सकता

---

🔁 Simple Diagram:

---

🔶 2. MLP: Multi-layer Perceptron

➤ परिभाषा:

MLP एक feedforward artificial neural network है जिसमें एक या अधिक hidden layers होते हैं।

🏗️ संरचना:

Input → Hidden Layer(s) → Output
(हर layer में neurons होते हैं, और हर neuron activation function apply करता है)

---

📌 विशेषताएँ:

गुण	विवरण
Structure	2+ layers (input, hidden, output)
Use	Complex, non-linear problems
Training	Backpropagation + Gradient Descent
Activation	ReLU, sigmoid, tanh, softmax

---

🔁 MLP Diagram (Structure):

---

💻 PyTorch में एक सरल MLP कोड:

import torch.nn as nn

class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(3, 5),   # Input layer → Hidden
            nn.ReLU(),
            nn.Linear(5, 1),   # Hidden → Output
            nn.Sigmoid()
        )

    def forward(self, x):
        return self.net(x)

---

🔄 तुलना तालिका: Perceptron vs MLP

विशेषता	Perceptron	MLP
Layers	Single	Multiple (hidden included)
Activation	Step/Sigmoid	ReLU, Sigmoid, Tanh, Softmax
Data Handling	केवल linearly separable	Complex, non-linear data
Learning	Simple weight update	Backpropagation algorithm

---

🎯 Learning Summary:

• Perceptron एक सबसे सरल Neural Network है।
• MLP में Hidden layers होने से यह complex pattern सीख सकता है।
• Deep Learning में MLP सबसे बुनियादी और आधारभूत संरचना है।

---

📝 अभ्यास प्रश्न (Practice Questions):

1. Perceptron का गणितीय फ़ॉर्मूला क्या है?
2. Perceptron और MLP में मुख्य अंतर क्या है?
3. MLP में activation functions क्यों ज़रूरी होते हैं?
4. Perceptron XOR problem क्यों solve नहीं कर सकता?
5. एक सरल MLP में कितनी layers होती हैं?

(जैविक न्यूरॉन बनाम कृत्रिम न्यूरॉन)

---

🔹 1. Biological Neuron (जैविक न्यूरॉन) क्या होता है?

यह मानव मस्तिष्क की मूल इकाई है जो संकेतों (signals) को लेती है, प्रक्रिया करती है और अन्य न्यूरॉनों को भेजती है।

🔬 संरचना (Structure):

भाग	कार्य
Dendrites	Input signal लेते हैं
Cell Body (Soma)	Input को process करता है
Axon	Output signal को भेजता है
Synapse	दो neurons के बीच signal पास करता है

🧠 कार्यप्रणाली:

• जब कुल Input signal एक Threshold से ऊपर जाता है, तब neuron “Fire” करता है (Signal भेजता है)।

---

🔹 2. Artificial Neuron (कृत्रिम न्यूरॉन)

Deep Learning में Artificial Neuron का उपयोग किया जाता है, जो Biological neuron से प्रेरित है लेकिन गणितीय होता है।

🔢 कार्यप्रणाली:

• xi​: Inputs
• wi: Weights
• b: Bias
• f: Activation function
• y: Output

---

🔁 तुलनात्मक तालिका (Comparison Table)

विशेषता	जैविक न्यूरॉन	कृत्रिम न्यूरॉन
संरचना	Dendrites, Axon, Synapse	Inputs, Weights, Activation
संकेत (Signal)	Electrochemical	Numerical (वास्तविक संख्या)
प्रसंस्करण	Threshold based firing	Weighted sum + Activation
सीखना	Synapse के बदलाव से	Weights update (Gradient Descent)
नेटवर्क	Biological Neural Network	Artificial Neural Network (ANN)

---

🧠 विज़ुअल तुलना (Diagram)

Biological Neuron:                        Artificial Neuron:

Input (Dendrites)                         x1, x2, x3 →  
         ↓                                      ↓
Cell Body (Summation)                    w1x1 + w2x2 + w3x3 + b
         ↓                                      ↓
Axon → Output                          Activation Function → Output

---

🔍 निष्कर्ष (Conclusion):

• Artificial Neurons inspired हैं Biological Neurons से, परंतु वे सरल गणितीय मॉडल हैं।
• एक Artificial Neuron सिर्फ एक छोटा सा भाग है Deep Learning नेटवर्क का, लेकिन उसका inspiration मानव मस्तिष्क से आया है।
• जैसा मानव मस्तिष्क सिखता है अनुभव से, वैसे ही ANN सिखता है डेटा से।

---

🎯 उद्देश्य (Objective Summary)

• जैविक न्यूरॉन की संरचना और कार्यप्रणाली समझना
• कृत्रिम न्यूरॉन का गणितीय स्वरूप जानना
• दोनों के बीच की समानता और भिन्नता पहचानना
• Deep Learning में इस संबंध का महत्व समझना

---

📝 अभ्यास प्रश्न (Practice Questions)

1. Dendrites और Axon का कार्य क्या होता है?
2. Artificial Neuron किस प्रकार का Input लेता है?
3. दोनों प्रकार के न्यूरॉन में signal कैसा होता है?
4. एक Artificial Neuron का गणितीय formula लिखिए।
5. कृत्रिम न्यूरॉन जैविक न्यूरॉन से कैसे प्रेरित है?

(न्यूरल नेटवर्क की मूल बातें)

---

🔷 1. परिचय (Introduction)

Neural Network एक ऐसा गणितीय मॉडल है जो इंसानी मस्तिष्क की तरह सीखने का प्रयास करता है। यह इनपुट को लेता है, layers के ज़रिए प्रोसेस करता है और फिर आउटपुट देता है।

Deep Learning = कई layers वाले Neural Network

---

🧱 2. Basic Structure of a Neural Network

एक Neural Network में मुख्यतः तीन प्रकार की layers होती हैं:

Layer Name	कार्य
Input Layer	बाहरी डेटा को लेती है
Hidden Layers	डेटा को प्रोसेस करती हैं
Output Layer	अंतिम निर्णय या अनुमान देती है

---

🔁 Working Flow:

Input → Weights × Input + Bias → Activation → Output

---

🧠 3. Perceptron – सबसे सरल Neural Unit

➤ परिभाषा:

Perceptron एक single-layer neural network है, जो binary classification कर सकता है।

Perceptron Formula:

जहाँ:

• xi​: Input
• wi: Weights
• b: Bias
• f: Activation Function (जैसे: Step Function)

---

💡 4. Activation Functions

Activation function यह तय करता है कि कोई neuron activate होगा या नहीं। यह non-linearity introduce करता है।

---

🔂 5. Forward Pass & Backpropagation

🔄 Forward Pass:

Input → Output तक की गणना
(Weights, Biases, Activation के साथ)

🔁 Backpropagation:

Loss को Output से Input की तरफ propagate करना
→ Gradient निकालना (Chain Rule)
→ Weights update करना (Gradient Descent)

---

💻 आवश्यक कोड: एक सिंपल Neural Network (PyTorch)

import torch
import torch.nn as nn

# Simple feedforward network
class SimpleNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(2, 4)  # Input layer to hidden
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(4, 1)  # Hidden to output

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        return self.fc2(x)

model = SimpleNN()
print(model)

---

📌 Visualization: Neural Network Structure

Input Layer: x1, x2
        ↓
Hidden Layer (Neurons)
        ↓
Activation (ReLU)
        ↓
Output Layer: ŷ

---

🎯 Chapter Objectives (लक्ष्य)

• Neural Network की मूल संरचना को समझना
• Perceptron की कार्यप्रणाली को जानना
• Activation Functions का महत्व जानना
• Forward और Backpropagation के बीच का संबंध समझना
• PyTorch में एक सरल मॉडल बनाना

---

📝 अभ्यास प्रश्न (Practice Questions)

1. Neural Network में तीन मुख्य layers कौन-सी होती हैं?
2. Perceptron का गणितीय फ़ॉर्मूला लिखिए और समझाइए।
3. ReLU और Sigmoid में क्या अंतर है?
4. Forward Pass और Backpropagation क्या होते हैं?
5. नीचे दिए गए कोड में कितने neurons hidden layer में हैं?

self.fc1 = nn.Linear(3, 5)

---