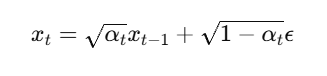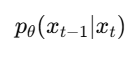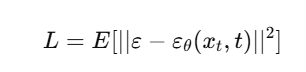मशीन लर्निंग (ML) क्या है?
🤖 मशीन लर्निंग क्या है?
Machine Learning (ML) कृत्रिम बुद्धिमत्ता (AI) का एक भाग है जिसमें कंप्यूटर को इस प्रकार सिखाया जाता है कि वह बिना स्पष्ट प्रोग्रामिंग के, अनुभव (data) से खुद सीख सके और निर्णय ले सके।
✅ सरल परिभाषा:
“Machine Learning एक तकनीक है जिसमें मशीनें स्वयं डेटा से सीखकर भविष्य की भविष्यवाणी करती हैं या निर्णय लेती हैं।”
🎓 एक लाइन में समझें:
AI = इंसानों जैसी बुद्धिमत्ता
ML = डेटा से सीखना और सुधार करना
📦 उदाहरण से समझें:
| परंपरागत प्रोग्रामिंग | मशीन लर्निंग |
|---|---|
| नियम (Rules) लिखकर प्रोग्राम बनाया जाता है | डेटा से मशीन खुद नियम सीखती है |
| “अगर” – “तो” (if-else) लॉजिक पर आधारित | एल्गोरिद्म डेटा से पैटर्न निकालते हैं |
उदाहरण:
- आप Amazon पर मोबाइल देखते हैं और आपको वही या उससे मिलते-जुलते मोबाइल सुझाव में दिखते हैं — यही Machine Learning है।
📊 मशीन लर्निंग कैसे काम करता है?
- डेटा एकत्र करें
- डेटा को साफ और तैयार करें
- उपयुक्त एल्गोरिद्म चुनें
- मॉडल को ट्रेन करें (Train the model)
- मॉडल को टेस्ट करें (Evaluate)
- नई जानकारी पर प्रेडिक्शन करें
🧠 मशीन लर्निंग क्यों ज़रूरी है?
- बड़े डेटा को मैन्युअली एनालाइज़ करना कठिन है
- तेजी से सटीक निर्णय लेना
- लगातार सुधार करने की क्षमता
🔍 वास्तविक दुनिया में कहां उपयोग होता है?
| क्षेत्र | उपयोग |
|---|---|
| हेल्थकेयर | रोगों की भविष्यवाणी |
| बैंकिंग | धोखाधड़ी की पहचान |
| ई-कॉमर्स | प्रोडक्ट सिफारिश |
| सोशल मीडिया | पोस्ट रैंकिंग, कंटेंट फिल्टर |
| कृषि | फसल की बीमारी की पहचान |
📌 निष्कर्ष / Conclusion:
- मशीन लर्निंग वह तकनीक है जो कंप्यूटर को “अनुभव” से सीखने की शक्ति देती है।
- यह आज की AI क्रांति की नींव है।
- अगले अध्यायों में हम इसके तीन प्रमुख प्रकारों (Supervised, Unsupervised, Reinforcement) को गहराई से समझेंगे।