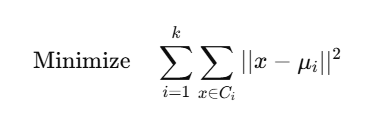K-Means Clustering एक Unsupervised Learning Algorithm है जो डेटा को k अलग-अलग clusters में बांटने का कार्य करता है, जहाँ हर cluster में डाले गए डेटा आपस में एक-दूसरे से अधिक समान होते हैं।
उदाहरण:
आप एक दुकान के ग्राहकों को उनके ख़रीदने की आदतों के आधार पर 3 समूहों में बाँटना चाहते हैं — High, Medium, और Low spenders।
🔶 उद्देश्य:
K-Means का लक्ष्य है:
Data Points को इस तरह से बांटना कि प्रत्येक Cluster का “Centroid” अपने Points से न्यूनतम दूरी पर हो।
📐 Mathematical Objective:
K-Means का Loss Function (Inertia) होता है:
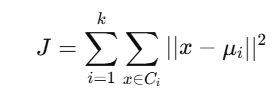
जहाँ:

🧠 Algorithm Steps:
- kkk initial centroids randomly चुनें
- हर point को सबसे पास वाले centroid के cluster में assign करें
- हर cluster का नया centroid calculate करें
- Step 2 और 3 को तब तक दोहराएं जब तक cluster assignment stable ना हो जाए
✅ Python Code (with Visualization):
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
# Dummy Data
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
# KMeans Model
model = KMeans(n_clusters=2, random_state=0)
model.fit(X)
# Output
print("Labels:", model.labels_) # Cluster assignments
print("Centroids:", model.cluster_centers_) # Cluster centers
# Visualization
plt.scatter(X[:, 0], X[:, 1], c=model.labels_, cmap='viridis')
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1],
c='red', marker='X', s=200, label='Centroids')
plt.title("K-Means Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.grid(True)
plt.show()
🔬 Elbow Method (Best k कैसे चुनें?)
Elbow Method यह देखने में मदद करता है कि कितने clusters लेने से सबसे अच्छी grouping मिलेगी।
📈 Plot Inertia vs k:
inertia = []
K = range(1, 10)
for k in K:
km = KMeans(n_clusters=k)
km.fit(X)
inertia.append(km.inertia_)
plt.plot(K, inertia, marker='o')
plt.xlabel('Number of Clusters k')
plt.ylabel('Inertia (Within Sum of Squares)')
plt.title('Elbow Method for Optimal k')
plt.show()
जहाँ graph में “elbow” बनता है — वही optimal k होता है।
🔎 Real Life Applications:
| Domain | Application Example |
|---|---|
| Marketing | Customer Segmentation |
| Healthcare | Disease pattern clustering |
| Finance | Risk Grouping / Fraud Detection |
| E-commerce | Product Recommendation (user grouping) |
⚖️ K-Means के फायदे और नुकसान:
✅ फायदे:
- Simple और Fast
- High-dimensional data पर काम करता है
- Easily scalable
❌ नुकसान:
- kkk पहले से पता होना चाहिए
- Non-spherical clusters को handle नहीं कर पाता
- Outliers पर sensitive होता है
- Local minima में फँस सकता है (initial centroid पर निर्भरता)
📊 Summary Table:
| Feature | K-Means |
|---|---|
| Type | Unsupervised Clustering |
| Input | Only Features (No Labels) |
| Output | Cluster IDs |
| Distance Metric | Euclidean Distance (Mostly) |
| Speed | Fast |
| Shape Assumption | Spherical Clusters |
📝 Practice Questions:
- K-Means का उद्देश्य क्या होता है?
- Loss function J का अर्थ क्या है?
- Elbow Method का क्या उपयोग है?
- K-Means कब खराब perform करता है?
- K-Means clustering में initialization क्यों महत्वपूर्ण होता है?