(रेखीय बीजगणित की मूल बातें: मैट्रिक्स, वेक्टर और टेन्सर)
🔷 2.1 परिचय (Introduction)
Deep Learning मॉडल, विशेष रूप से Neural Networks, मुख्य रूप से संख्याओं (numbers) के साथ काम करते हैं। इन संख्याओं को संगठित और प्रोसेस करने के लिए हम Linear Algebra की तकनीकों का उपयोग करते हैं।
🧮 2.2 वेक्टर (Vectors)
➤ परिभाषा:
वेक्टर एक ऐसी सूची है जिसमें संख्याएँ एक विशेष क्रम में होती हैं। यह 1D array होता है।
उदाहरण:
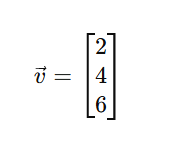
✅ उपयोग:
- Neural Network के inputs और weights को वेक्टर में संग्रहित किया जाता है।
- वेक्टर dot product और angle measurement में प्रयोग होते हैं।
🛠️ वेक्टर ऑपरेशन:
| क्रिया | उदाहरण |
|---|---|
| जोड़ | [1,2]+[3,4]=[4,6] |
| स्केलर गुणा | 3×[1,2]=[3,6] |
| डॉट प्रोडक्ट | [1,2]⋅[3,4]=1×3+2×4=11 |
🟦 2.3 मैट्रिक्स (Matrix)
➤ परिभाषा:
Matrix एक 2D array होता है जिसमें rows और columns होते हैं। यह वेक्टर का विस्तार है।
उदाहरण:
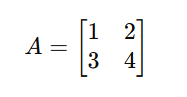
✅ उपयोग:
- Neural Networks में inputs, weights, और activations को Matrix के रूप में रखा जाता है।
- Matrix multiplication द्वारा layers के बीच data forward होता है।
🛠️ Matrix Operations:
| क्रिया | विवरण |
|---|---|
| Transpose | पंक्ति को स्तंभ में बदलना |
| Multiplication | m×n×n×p = m×p |
| Identity Matrix | I, जहां A⋅I=A |
| Inverse (A⁻¹) | केवल कुछ matrices के लिए संभव |
🧊 2.4 टेन्सर (Tensors)
➤ परिभाषा:
Tensors वेक्टर और मैट्रिक्स का सामान्यीकृत रूप है।
- वेक्टर = 1D टेन्सर
- मैट्रिक्स = 2D टेन्सर
- 3D+ arrays = Higher Order Tensors
उदाहरण:
import torch
x = torch.rand(2, 3, 4) # 3D Tensor (2×3×4)
✅ उपयोग:
- Deep Learning frameworks (जैसे PyTorch, TensorFlow) का मुख्य डेटा structure टेन्सर है।
- Multidimensional डेटा को efficiently store और process करने के लिए।
🔄 2.5 Vector, Matrix, Tensor तुलना तालिका:
| गुण | वेक्टर | मैट्रिक्स | टेन्सर |
|---|---|---|---|
| आयाम (Dimensions) | 1D | 2D | ND (3D, 4D…) |
| रूप | [x,y,z] | [[a,b],[c,d]] | [[[]]] |
| उपयोग | Input, Output | Layer Weights | Images, Sequences |
🔧 2.6 Deep Learning में Linear Algebra का प्रयोग
| क्षेत्र | Linear Algebra उपयोग |
|---|---|
| Input Data | Vectors / Tensors |
| Layer Weights | Matrix Multiplication |
| Feature Extraction | Dot Product |
| Backpropagation | Gradient Computation using Matrix derivatives |
| Images | Tensors of size (Channels × Height × Width) |
🧠 उदाहरण:
PyTorch Code Example (Matrix multiplication):
import torch
A = torch.tensor([[1., 2.], [3., 4.]])
B = torch.tensor([[2., 0.], [1., 2.]])
result = torch.matmul(A, B)
print("Matrix A × B =\n", result)
Output:
Matrix A × B =
tensor([[ 4., 4.],
[10., 8.]])
📚 अभ्यास प्रश्न (Quiz)
❓Q1. वेक्टर और मैट्रिक्स में क्या अंतर है?
✅ वेक्टर 1D array है, जबकि मैट्रिक्स 2D array है।
❓Q2. Dot Product का उपयोग Neural Network में कहाँ होता है?
✅ Input और Weights के बीच के संबंध की गणना के लिए
❓Q3. टेन्सर क्या होता है?
✅ एक ND array जो वेक्टर और मैट्रिक्स दोनों को generalize करता है।
❓Q4. PyTorch या TensorFlow किस डेटा structure का उपयोग करते हैं?
✅ Tensor
✅ निष्कर्ष (Conclusion)
Linear Algebra Deep Learning की गणितीय रीढ़ है।
- Vectors input/output को दर्शाते हैं
- Matrices weights और connections को संभालते हैं
- Tensors complex data (जैसे images, sequences) को efficiently represent करते हैं
इस अध्याय की समझ आगे के मॉडल्स, training और optimization को गहराई से समझने में मदद करेगी।
