PCA – Principal Component Analysis

PCA (Principal Component Analysis) एक statistical technique है जो high-dimensional data को कम dimensions में project करके उसका meaningful structure retain करती है।

उदाहरण के लिए:
अगर आपके पास 100 features हैं, लेकिन असल में केवल 2 features पूरे pattern को explain कर सकते हैं — तो PCA उन्हीं 2 को चुनता है।

---

🔶 उद्देश्य:

• Features की संख्या को घटाना (Dimensionality Reduction)
• Data में मौजूद variance को अधिकतम बनाए रखना
• Visualization को आसान बनाना
• Noise को घटाना और Model को Fast बनाना

---

📐 Core Idea (Mathematical):

PCA का लक्ष्य होता है:

ऐसे नए axes (Principal Components) खोजना जो original data में सबसे अधिक variance को capture करें।

🎯 Objective:

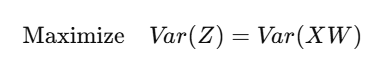
जहाँ:

• X: Centered data matrix
• W: Projection matrix (eigenvectors)
• Z: Projected data (principal components)

---

🧮 Step-by-Step Working:

Standardize the Data
(mean = 0, std = 1)

Covariance Matrix Calculate करो

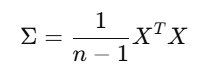
Eigenvalues और Eigenvectors निकालो

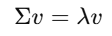
Top-k Eigenvectors को चुनो (सबसे बड़ी eigenvalues वाले)

Data को Project करो new space में:

---

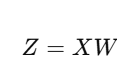
✅ Python Code (Sklearn + Visualization):

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# Load sample data
data = load_iris()
X = data.data
y = data.target

# PCA with 2 components
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Plot
plt.figure(figsize=(8,6))
plt.scatter(X_pca[:,0], X_pca[:,1], c=y, cmap='viridis')
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("PCA: Iris Dataset")
plt.grid(True)
plt.show()

---

📊 Explained Variance:

PCA बताता है कि हर component कितना information retain करता है:

print(pca.explained_variance_ratio_)

उदाहरण Output:

[0.9246, 0.0530] → यानी कुल 97.76% variance केवल 2 components से explain हो गया

---

🔎 कब इस्तेमाल करें PCA?

Case	उपयोग
बहुत सारे features हों	✅
Model slow या overfit कर रहा हो	✅
Feature correlation ज़्यादा हो	✅
Features sparse हों (जैसे TF-IDF)	✅

---

⚠️ Limitations:

Limitation	Explanation
Interpretability कम हो जाती है	PCs original features से अलग होते हैं
केवल linear patterns detect करता है	Complex nonlinear pattern नहीं देख सकता
Scaling आवश्यक है	बिना scaling result गलत हो सकता है

---

📊 Summary Table:

Feature	PCA
Type	Dimensionality Reduction
Preserves	Maximum Variance
Based On	Eigenvalues & Eigenvectors
Suitable For	High-dimensional, numeric data
Output	Reduced dimension components

---

📝 Practice Questions:

1. PCA का उद्देश्य क्या होता है?
2. Covariance matrix किस लिए बनाई जाती है?
3. Eigenvectors और Eigenvalues का क्या अर्थ है PCA में?
4. Explained Variance Ratio क्या दर्शाता है?
5. PCA कब काम नहीं करता?